Cracking the Code of Concept Learning: Find-S and Candidate Elimination Algorithms
Welcome, future AI wizards! If you're reading this, you've probably wondered how machines learn to classify things—like how Netflix knows you're a rom-com person or how your phone recognizes your...
Welcome, future AI wizards! If you're reading this, you've probably wondered how machines learn to classify things—like how Netflix knows you're a rom-com person or how your phone recognizes your face even with that questionable quarantine haircut. Today, we're diving into two foundational algorithms that kickstarted the whole concept learning party: Find-S and Candidate Elimination.
Think of these algorithms as the training wheels of machine learning—simple, elegant, and surprisingly effective at teaching machines to learn patterns from examples. They're the algorithms your professors love because they're easy to explain, and you'll (grudgingly) love because they actually make sense.
# What's This "Concept Learning" Business Anyway?
Before we jump in, let's get our terminology straight. Concept learning is the task of acquiring the definition of a general category from specific examples. It's like learning what makes a "good pizza"—you see enough examples (thin crust, extra cheese, not pineapple), and eventually, your brain forms a hypothesis about what pizza should be.
In machine learning terms, we're trying to find a hypothesis (a rule) that correctly classifies examples as positive (✓ yes, this is our concept) or negative (✗ nope, not our concept). Both Find-S and Candidate Elimination are supervised learning approaches—meaning they learn from labeled examples you provide.
# Meet Our Dataset: The "Enjoy Sport" Problem
Let's work with a classic example that both algorithms can tackle. Imagine we're trying to predict whether someone will enjoy playing their favorite sport based on weather conditions.
Our attributes:
- Sky: Sunny, Cloudy, Rainy
- Temperature: Warm, Cold
- Humidity: Normal, High
- Wind: Strong, Weak
- Water: Warm, Cool
- Forecast: Same, Change
Training Examples:
| Example | Sky | Temperature | Humidity | Wind | Water | Forecast | Enjoy Sport? |
|---|---|---|---|---|---|---|---|
| 1 | Sunny | Warm | Normal | Strong | Warm | Same | Yes ✓ |
| 2 | Sunny | Warm | High | Strong | Warm | Same | Yes ✓ |
| 3 | Rainy | Cold | High | Strong | Warm | Change | No ✗ |
| 4 | Sunny | Warm | High | Strong | Cool | Change | Yes ✓ |
Now, let's see how our two algorithms handle this challenge!
# The Find-S Algorithm: The Optimistic Generalizer
# The Philosophy
Find-S is the embodiment of toxic positivity in algorithm form—it only looks at positive examples and completely ignores negative ones. It's like that friend who only remembers the good times and conveniently forgets when you both got food poisoning from that sketchy taco truck.
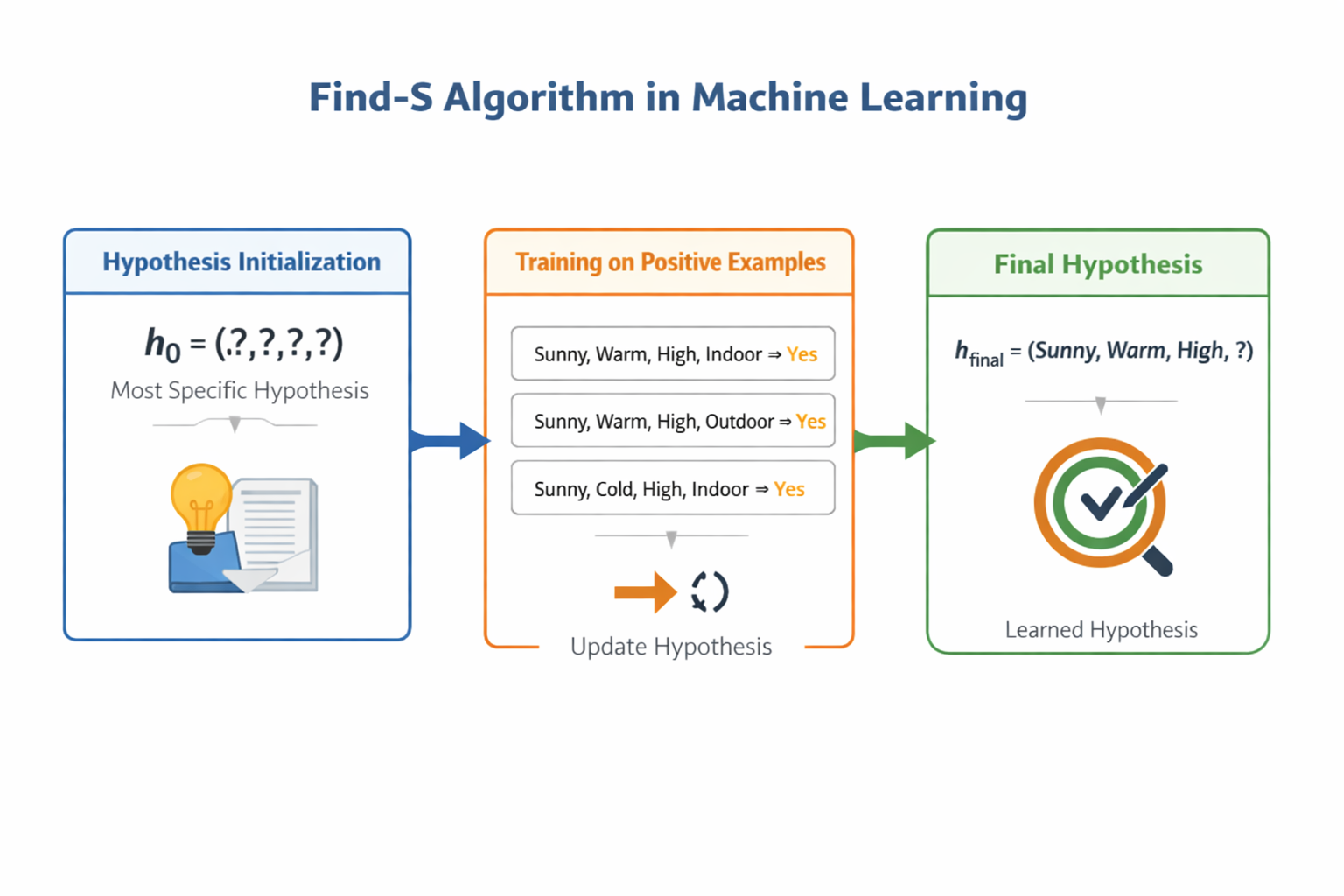
The algorithm starts with the most specific hypothesis possible (represented as ⟨∅, ∅, ∅, ∅, ∅, ∅⟩, meaning "nothing satisfies this") and gradually generalizes it each time it encounters a positive example.
# How Find-S Works: The Algorithm
Step-by-step process:
- Initialize hypothesis h to the most specific: h = ⟨∅, ∅, ∅, ∅, ∅, ∅⟩
- For each positive training example: If an attribute value matches h, keep it; If it doesn't match, generalize that attribute to "?" (meaning "any value works")
- Ignore all negative examples (yes, really!)
- Return the final hypothesis after processing all positive examples
# Find-S in Action: Step-by-Step Execution
Initial Hypothesis: h₀ = ⟨∅, ∅, ∅, ∅, ∅, ∅⟩
Processing Example 1 (Sunny, Warm, Normal, Strong, Warm, Same → Yes):
- Since this is the first positive example, replace all ∅ with actual values
- h₁ = ⟨Sunny, Warm, Normal, Strong, Warm, Same⟩
Processing Example 2 (Sunny, Warm, High, Strong, Warm, Same → Yes):
- Sky: Sunny = Sunny ✓ (keep it)
- Temperature: Warm = Warm ✓ (keep it)
- Humidity: High ≠ Normal ✗ (generalize to ?)
- Wind: Strong = Strong ✓ (keep it)
- Water: Warm = Warm ✓ (keep it)
- Forecast: Same = Same ✓ (keep it)
- h₂ = ⟨Sunny, Warm, ?, Strong, Warm, Same⟩
Processing Example 3 (Rainy, Cold, High, Strong, Warm, Change → No):
- It's a negative example—Find-S ignores it completely! h₃ = h₂
Processing Example 4 (Sunny, Warm, High, Strong, Cool, Change → Yes):
- Sky: Sunny = Sunny ✓
- Temperature: Warm = Warm ✓
- Humidity: High = ? ✓ (already generalized)
- Wind: Strong = Strong ✓
- Water: Cool ≠ Warm ✗ (generalize to ?)
- Forecast: Change ≠ Same ✗ (generalize to ?)
- Final Hypothesis: h_final = ⟨Sunny, Warm, ?, Strong, ?, ?⟩
# What Find-S is Telling Us
Our final hypothesis says: "Someone will enjoy sport when it's Sunny, Warm, with Strong wind—humidity, water temperature, and forecast don't matter".
# Find-S: The Good, The Bad, and The Ugly
Advantages:
- Simple as your morning coffee order—easy to implement and understand
- Computationally efficient; one pass through the data and you're done
- Guaranteed to find a hypothesis consistent with positive examples
Limitations:
- Completely ignores negative examples (which is like learning to drive by only studying successful trips and never learning from crashes)
- Can't tell you if the hypothesis is the only one or the best one
- Sensitive to noisy data—one mislabeled example can derail everything
- No backtracking; once generalized, you can't get more specific again
# The Candidate Elimination Algorithm: The Perfectionist
# The Philosophy
If Find-S is an optimist, Candidate Elimination is a thorough detective who maintains a version space—a set of ALL hypotheses consistent with the training data. Instead of committing to one hypothesis, it keeps track of boundaries that contain all possible valid hypotheses.
The algorithm maintains two boundaries:
- S (Specific Boundary): The most specific hypotheses consistent with data
- G (General Boundary): The most general hypotheses consistent with data
Every valid hypothesis lives somewhere between S and G—this is your version space.
# How Candidate Elimination Works: The Algorithm
Initialization:
- S = {⟨∅, ∅, ∅, ∅, ∅, ∅⟩} (most specific)
- G = {⟨?, ?, ?, ?, ?, ?⟩} (most general—everything is acceptable)
For each training example:
If positive example:
- Remove any hypothesis from G that doesn't match this example
- Generalize S minimally to cover this example (if needed)
- Remove from S any hypothesis more general than another in S
If negative example:
- Remove any hypothesis from S that matches this example
- Specialize G minimally to exclude this example
- Remove from G any hypothesis more specific than another in G
Terminate when: S and G converge to the same hypothesis, or no more examples remain
# Candidate Elimination in Action: Step-by-Step Execution
Initial State:
- S₀ = {⟨∅, ∅, ∅, ∅, ∅, ∅⟩}
- G₀ = {⟨?, ?, ?, ?, ?, ?⟩}
Processing Example 1 (Sunny, Warm, Normal, Strong, Warm, Same → Yes):
- Positive example! Generalize S to include it
- S₁ = {⟨Sunny, Warm, Normal, Strong, Warm, Same⟩}
- G₁ = {⟨?, ?, ?, ?, ?, ?⟩} (unchanged—already covers everything)
Processing Example 2 (Sunny, Warm, High, Strong, Warm, Same → Yes):
- Positive example! S doesn't cover it (Humidity: High ≠ Normal)
- Generalize S minimally: S₂ = {⟨Sunny, Warm, ?, Strong, Warm, Same⟩}
- G₂ = {⟨?, ?, ?, ?, ?, ?⟩} (still unchanged)
Processing Example 3 (Rainy, Cold, High, Strong, Warm, Change → No):
- Negative example! Now G must be specialized to exclude this
- The most general hypothesis ⟨?, ?, ?, ?, ?, ?⟩ would classify this as positive (wrong!)
- We need to specialize G by constraining attributes that differ from our S
- G₃ = {⟨Sunny, ?, ?, ?, ?, ?⟩, ⟨?, Warm, ?, ?, ?, ?⟩, ⟨?, ?, ?, ?, ?, Same⟩}
- (These say: "Sky must be Sunny" OR "Temp must be Warm" OR "Forecast must be Same")
- S₃ = S₂ (unchanged—S already doesn't match this negative example)
Processing Example 4 (Sunny, Warm, High, Strong, Cool, Change → Yes):
- Positive example! S doesn't match (Water: Cool ≠ Warm, Forecast: Change ≠ Same)
- Generalize S: S₄ = {⟨Sunny, Warm, ?, Strong, ?, ?⟩}
- Update G to remove hypotheses inconsistent with this positive example
- ⟨?, ?, ?, ?, ?, Same⟩ is removed (Forecast is Change here, not Same)
- G₄ = {⟨Sunny, ?, ?, ?, ?, ?⟩, ⟨?, Warm, ?, ?, ?, ?⟩}
Final Version Space:
- S_final = {⟨Sunny, Warm, ?, Strong, ?, ?⟩}
- G_final = {⟨Sunny, ?, ?, ?, ?, ?⟩, ⟨?, Warm, ?, ?, ?, ?⟩}
The version space contains all hypotheses between these boundaries. Notice that S_final is MORE specific than both hypotheses in G_final, meaning there are multiple valid hypotheses that fit the data!
# What Candidate Elimination is Telling Us
The algorithm says: "Based on the data, 'enjoying sport' could mean needing Sunny weather, OR it could mean needing Warm temperature, OR it could be the combination in S". Unlike Find-S, it acknowledges uncertainty and maintains multiple possibilities.
# Candidate Elimination: Strengths and Weaknesses
Advantages:
- Uses BOTH positive and negative examples—a complete learner
- Maintains all consistent hypotheses, not just one
- Can detect when data is inconsistent or when target concept isn't learnable
- More robust for complex concept learning tasks
Limitations:
- Computationally expensive; managing S and G boundaries can be intensive for large hypothesis spaces
- Assumes noise-free data; a single mislabeled example can corrupt the version space
- Requires concepts expressible as conjunctions of attributes (no disjunctions like "A OR B")
- Can fail if the target concept isn't in the hypothesis space
# Head-to-Head: Find-S vs. Candidate Elimination
| Aspect | Find-S Algorithm | Candidate Elimination Algorithm |
|---|---|---|
| Learning approach | Only learns from positive examples | Uses both positive and negative examples |
| Output | Single most specific hypothesis | Version space (multiple hypotheses) |
| Hypothesis representation | Moves from specific to general | Maintains specific (S) and general (G) boundaries |
| Complexity | Simple, one-pass algorithm | More complex, manages two boundary sets |
| Robustness to noise | Low; very sensitive to noisy data | Low; assumes noise-free examples |
| Computational efficiency | High; fast execution | Lower; computationally intensive |
| Handling inconsistency | Cannot detect inconsistencies | Can detect when hypotheses are inconsistent |
| Refinement capability | No backtracking; only generalizes | Iterative refinement of both boundaries |
| Best use case | Small, clean datasets with clear patterns | Complex tasks requiring hypothesis uncertainty |
# The Role of These Algorithms in Machine Learning
You might be thinking: "These seem pretty basic. Why are we learning algorithms from the ML Stone Age?" Great question, skeptical student!
# Historical Significance
Find-S and Candidate Elimination are the founding fathers of concept learning. They introduced fundamental ideas that influenced modern machine learning:
- Hypothesis space search: The idea that learning is searching through possible hypotheses
- Inductive bias: Understanding what assumptions algorithms make about data
- Version spaces: The concept that multiple hypotheses can explain data, pioneering ensemble methods
# Pedagogical Value
These algorithms are teaching tools that illustrate core ML principles without the complexity of neural networks or gradient descent. They help you understand:
- How machines generalize from specific examples
- The bias-variance tradeoff in simple terms
- Why handling both positive and negative examples matters
- The computational tradeoffs in algorithm design
# Practical Applications (Yes, Really!)
While you won't deploy Find-S in production at Google, the principles apply to:
- Rule-based systems: Expert systems in healthcare and finance still use concept learning approaches
- Feature engineering: Understanding which attributes matter helps in feature selection
- Explainable AI: These algorithms produce interpretable rules, unlike black-box neural networks
- Baseline models: Simple algorithms provide benchmarks for complex models
# When to Use Which Algorithm?
Choose Find-S when:
- You have abundant positive examples but few/no negative examples
- You need quick results and computational efficiency is critical
- Your hypothesis space is small and well-defined
- Interpretability matters more than perfect accuracy
- You're building a baseline or proof-of-concept
Choose Candidate Elimination when:
- You have balanced positive and negative examples
- You need to understand the space of possible solutions, not just one answer
- Data quality is high (low noise)
- The task requires understanding hypothesis uncertainty
- You can afford the computational cost for better robustness
Choose neither when:
- Your data is noisy or has missing values (both fail here)
- You need disjunctive concepts ("A OR B" rules)
- The hypothesis space is continuous or infinite
- You have massive datasets (modern deep learning is better)
# The Bigger Picture: Where Do We Go From Here?
These algorithms set the stage for everything that came after. Modern machine learning borrowed their DNA:
- Decision trees extended the idea of attribute-based learning with hierarchical structures
- Version space algebra evolved into ensemble methods like Random Forests
- Support Vector Machines refined the concept of hypothesis boundaries
- Even neural networks perform a sophisticated version of hypothesis space search through gradient descent
Understanding Find-S and Candidate Elimination gives you the conceptual foundation to grasp why modern algorithms work the way they do. They're the "Hello World" of machine learning—simple, fundamental, and surprisingly profound once you get them.
# Wrapping Up: Your Concept Learning Toolkit
Both Find-S and Candidate Elimination tackle the same problem with different philosophies. Find-S is your quick-and-dirty prototyper—fast, simple, but limited. Candidate Elimination is your meticulous researcher—thorough, principled, but demanding.
Neither is perfect. Both assume noise-free data (good luck with that in the real world). Both struggle with complex hypothesis spaces. But together, they teach you the fundamental dance of machine learning: balancing specificity and generalization, handling evidence, and managing uncertainty.
As you move forward in your ML journey, you'll encounter algorithms that make these look like Stone Age tools. But remember—every sophisticated model is just doing a fancier version of what Find-S and Candidate Elimination pioneered: learning patterns from examples, one hypothesis at a time.
Now go forth and generalize responsibly! And remember—when your neural network fails to converge at 3 AM before your project demo, at least Find-S would've given you something to present. Sometimes, simple is beautiful.
Pro tip for your exams: Professors LOVE asking you to trace these algorithms step-by-step. Practice with different datasets, understand the intuition, and you'll ace those questions while your classmates are still figuring out which boundary is which. You're welcome! 😉
Have questions about concept learning or want more ML algorithm breakdowns? Drop them in the comments below! And if this helped you understand these algorithms better than your textbook did, share it with your study group—they'll thank you during finals.

About the Author
Dr. Himanshu Rai is an Assistant Professor in Computer Science & Engineering at SRM Institute of Science and Technology, specializing in Machine Learning, Artificial Intelligence, and Data Science. She is passionate about advancing research in computational intelligence and mentoring students.